- Dalam suatu permainan pelambungan dadu, 2 Dadu dilambungkan bersama. Jika mata dadu yang muncul pada sisi dadu pertama ditambah mata yang muncul pada sisi dadu kedua kurang dari 6, maka pemain akan mendapat Hadiah Rp 750,00 dan untuk kejadian lainnya pemain tidak mendapat hadiah. Berapa harapan matematika pemain ?
Jawab :
Misal, d1 = banyak mata dadu yang muncul pada dadu 1.
d2 = banyak mata dadu yang muncul pada dadu 2
P1(d1+d2<6) = P{(1,1),(1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (3,1), (3,2), (4,1)}
P1 = 
dan D1 = Rp 750,00,-
E(x)=P1 x D1 =
x Rp 750,00 = Rp 208,33,-
- Pada suatu saat probablitas dari turun hujan 2/5, dimana Aliruddin saat ini tidak menjual es. Jika hari tidak hujan (cerah) Aliruddin mendapat keuntungan Rp.3500,00. tetapi jika hari hujan Aliruddin kehilangan keuntunga
Jawab :
P1= Probabilitas hari tidak hujan = 
P2= Probabilitas hari hujan = 
Jika hari tidak hujan, Aliruddin mendapat keuntungan Rp 3500,00 dan jika hari hujan, Aliruddin kehilangan keuntungan Rp 3000,00.
D1 = Rp 3500,00
D2 = Rp 3000,00
Maka, E(x) = P1D1 + P2D2
= (
x Rp 3500,00) + (
x Rp 3000,00)
= Rp 900,00
Maka harapan Aliruddin dalam kejadian ini adalah Rp.900,00
- Dalam suatu permainan menembak sasaran hadiah pertama disediakan sebesar Rp.100.000,00 diberikan kepada pemain yang dapat mengenai sasaran 5x berturut-turut dan hadiah kedua sebesar Rp. 75000,00 diberikan kepada pemain mengenai sasaran 3x berturut-turut dalam 5x tembakan. Berapa harapan matematika Efendi ?
Jawab :
Misal : M = mengenai sasaran.
m = tidak mengenai sasaran.
Berarti, P(M) =
dan P(m) = 
Misal, P1= Probabilitas memenangkan hadiah I
P2 = Probabilitas memenaqngkan hadiah II
Maka, P1 = P( M.M.M.M.M)
P1 = (
. . . . ) = 
P2= P ( m.m.M.M.M + M.m.m.M.M + M.M.m.m.m)
= ( . . . . +. .. . +.. . . )
= 
Hadiah I = D1= Rp 100.000,00,-
Hadiah II = D2= Rp 75.000,00,-
Jadi, E(x) = P1D1 + P2D2
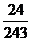=(x Rp 100.000,00,- ) + ( x Rp 75.000,00,- )
= Rp 20576,12,-
- Tujuh buah dadu dilambungkan bersama 1 kali. X menyatakan banyaknya mata ganjil yang muncul. Tentukan
- Rumus untuk Distribusi Probablitas.
- Harapan Matematikanya.
Jawab :
- B(x,7,
) = 
Untuk x = 0,1,2,3,4,5,6,7.
- f(0) =
= 
f(1) = 
= 
f(2) = 
= 
f(3) = 
= 
f(4) = 
=
f(5) = 
=
f(6) = 
=
f(7) = 
=
E(x) = 0. + 1. + 2. + 3. + 4. + 5. + 6. + 7.
E(x) = 
= 3,5
5. Tentukan Harapan matematika Variabel- Variabel Random yang mempunyai kerapatan
Probablitas
· 2-x Untuk 1≤ x < 2
F(X) = x-2 Untuk 2≤ x ≤ 3
0 Untuk x yang lain.
Jawab :
E(x) = 
= 
x (0) dx + 
x(2-x) dx + 
x(x-2)dx + 
x.0 dx
= x(2-x) dx + x(x-2) dx
= (2x-x2) dx + (x2-2x) dx
= 
+ 
= 
- 
+ 
- 
= 
- 
+ 
- 
= -2 + 
= 
+
= 
= 2
